Догадка гольдбаха (версия 2.1)
Догадка Гольдбаха была высказана прусским математиком Кристианом Гольдбахом в 1742 году в письме Леонарду Эйлеру и формулируется следующим образом: "Каждое четное число, большее двух, может быть представлено в виде суммы двух простых чисел." Попытки доказать истинность Догадки Гольдбаха или подтвердить невозможность такого доказательства до настоящего времени успеха не имели. Предыдущая попытка от assembler.ru тоже была не совсем удачной. Нынешняя кажется более убедительной. Здесь используются те же идеи, но уже нет никаких кирпичей, зато есть довольно внятная математика, устранены кое-какие проблемы и выявлены новые существенные обстоятельства.
Еще одна очень интересная попытка доказательства представлена Тимом Туманным. Всем интересующимся этой проблемой рекомендуется к изучению и обсуждению в первую очередь.
Основная идея предлагаемого доказательства заключается в том, чтобы сопоставить каждому четному числу E некоторую величину SE, заведомо меньшую, чем действительное число пар простых чисел, дающих в сумме число E. Четное число E, для которого значение SE > 1, обязательно будет иметь не менее одной пары простых чисел, дающих в сумме число E. Если условие SE > 1 выполняется для всех E, то Догадка Гольдбаха верна.
Каждое четное число E можно представить в виде суммы двух чисел с помощью E/2 уникальных пар. Необходимо исключить из этого количества все пары, в которых содержатся не простые числа. При определении, является ли число простым, будем руководствоваться правилом: число является простым, если не делится на все простые числа, меньшие или равные корню квадратному из этого числа.
Возьмем для примера четное число 78. Его можно представить в виде суммы двух чисел с помощью 39 пар: 1+77 2+76 3+75 4+74 5+73 6+72 7+71 8+70 9+69 10+68 11+67 12+66 13+65 14+64 15+63 16+62 17+61 18+60 19+59 20+58 21+57 22+56 23+55 24+54 25+53 26+52 27+51 28+50 29+49 30+48 31+47 32+46 33+45 34+44 35+43 36+42 37+41 38+40 39+39.
Исключим из числа имеющихся пар те, которые содержит числа, делимые на 2. Останется либо половина от определенного в п.2 числа пар (как, например, для E=16: 1+15 3+13 5+11 7+9), либо больше половины (как для E=18: 1+17 3+15 5+13 7+11 9+9). Воспользуемся первым случаем, потому что эта величина меньше, и, следовательно, соответствует принятому методу доказательства. Итак, после исключения пар, числа в которых делятся на 2, останется
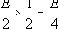
В примере с числом 78 на этом этапе подлежат исключению 19 пар: 1+77 2+76 3+75 4+74 5+73 6+72 7+71 8+70 9+69 10+68 11+67 12+66 13+65 14+64 15+63 16+62 17+61 18+60 19+59 20+58 21+57 22+56 23+55 24+54 25+53 26+52 27+51 28+50 29+49 30+48 31+47 32+46 33+45 34+44 35+43 36+42 37+41 38+40 39+39.
Остается 20 пар: 1+77 3+75 5+73 7+71 9+69 11+67 13+65 15+63 17+61 19+59 21+57 23+55 25+53 27+51 29+49 31+47 33+45 35+43 37+41 39+39.
Предлагаемая оценка дает значение 19.5, что меньше фактического числа оставшихся пар и согласуется с принятой методикой доказательства.
Исключим из числа оставшихся после п.3 пар те, которые содержат числа, делимые на 3. Следует оценить, какое наименьшее количество пар останется. Поскольку число 2, использовавшееся в предыдущем пункте, и число 3 - простые, то можно было бы утверждать, что при достаточно больших E это количество будет приближаться к 1/3 части от числа пар, оставшихся после предыдущего пункта. Однако количество пар должно выражаться натуральным числом. Следовательно, имеют место ошибки округления. Чтобы учесть их в наихудшем варианте, вычтем из результата оценки единицу:
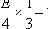
В примере с числом 78 на этом этапе подлежат исключению 7 пар: 1+77 3+75 5+73 7+71 9+69 11+67 13+65 15+63 17+61 19+59 21+57 23+55 25+53 27+51 29+49 31+47 33+45 35+43 37+41 39+39.
Остается 13 пар: 1+77 5+73 7+71 11+67 13+65 17+61 19+59 23+55 25+53 29+49 31+47 35+43 37+41.
Предлагаемая оценка дает значение 5.5, что меньше фактического числа оставшихся пар и согласуется с принятой методикой доказательства.
Продолжая рассуждения, исключим из оставшихся после п.4 пар те, которые содержат числа, делимые на 5. Первое число в каждой паре делится на 5 примерно в 1/5 случаев. Второе число также делится на 5 тоже примерно в 1/5 случаев, не обязательно других и не обязательно тех же самых. В худшем варианте те и другие - разные случаи, и тогда пар, в которых ни одно из чисел не делится на 5, примерно 3/5 от числа, оставшегося после предыдущего пункта. С учетом ошибки округления их количество:
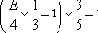
В примере с числом 78 на этом этапе подлежат исключению 4 пары: 1+77 5+73 7+71 11+67 13+65 17+61 19+59 23+55 25+53 29+49 31+47 35+43 37+41.
Остается 9 пар: 1+77 5+73 7+71 11+67 17+61 19+59 29+49 31+47 37+41.
Предлагаемая оценка дает значение 2.3, что меньше фактического числа оставшихся пар и согласуется с принятой методикой доказательства.
(Следует обратить внимание на наличие в числе остающихся пары 5+73. Она не подлежит исключению на этом этапе, так как число 5 - простое.)
На следующем шаге исключаются пары, которые содержат числа, делимые на 7. После этого в наихудшем случае остается количество пар, описываемое выражением:
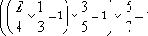
В примере с числом 78 на этом этапе подлежат исключению 2 пары: 1+77 5+73 7+71 11+67 17+61 19+59 29+49 31+47 37+4.
Остается 7 пар: 5+73 7+71 11+67 17+61 19+59 31+47 37+41.
Предлагаемая оценка дает значение ~0.643, что меньше фактического числа оставшихся пар. Вместе с тем это число меньше 1, то есть наличие пар простых слагаемых для числа 78 нашим доказательством не гарантируется (оно подтверждено эмпирически). Однако это еще не значит, что доказательство неверно.
Все числа в полученных парах - простые, так как использованное на этом шаге число 7 является наибольшим простым числом, меньшим, чем квадратный корень из 78. Дальнейшие итерации для числа 78 выполнять нет необходимости.
Обобщая сказанное выше, каждому E можно сопоставить значение, величина которого никогда не превысит фактическое количество пар простых чисел:
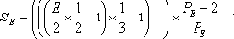
где PE - наибольшее простое число, удовлетворяющее условию
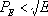
Работу этого выражения можно проиллюстрировать предлагаемой программой. Программа работает в броузерах, поддерживающий JavaScript и фреймы. Она моделирует процесс отсева пар, содержащих не простые числа. При этом вычисляется оценка количества остающихся пар на каждом шаге отсева (step SE[i]) и накопленная оценка (partial SE(i)). Пробуя различные E, можно убедиться, что ни та, ни другая оценка не превышают реального количества остающихся пар.
Очевидно, значения SE образуют последовательность на множестве простых чисел. В контексте доказательства достаточно выполнить ее анализ, пользуясь расчетом. Видно, что значения SE, начиная с некоторого момента, устойчиво превышают 1 и возрастают. В точках, где вступает в силу новое PE, наблюдаются отрицательные девиации значений последовательности SE. Эти девиации обусловлены тем, что в этих точках в выражении для SE появляется новый множитель (PE-2)/PE и вычитается еще одна единица. Но их влияние с ростом E, очевидно, постоянно уменьшается, поскольку E возрастает линейно, а их появление обусловлено корнем квадратным из E, и, кроме того, (PE-2)/PE стремится к 1. Следовательно, начиная с некоторого момента, девиации никогда не станут настолько велики, чтобы значение SE стало меньше 1.
Вывод. Каждому четному числу E, начиная с некоторого, можно поставить в соответствие значение SE такое, что оно заведомо меньше фактического числа пар простых чисел, дающих в сумме число E, и одновременно больше 1. Следовательно, для каждого такого четного числа существует не менее одной пары простых чисел, дающих в сумме это число. Наличие таких пар для чисел E, меньших указанного, подтверждается эмпирически. Догадка Гольдбаха доказана.
Предлагаемое доказательство, к сожалению, нельзя считать окончательным. Несмотря на то, что оценка SE кажется надежно меньшей, чем реальное количество пар простых слагаемых, существует обстоятельство, снижающее уровень доверия к ней. Это обстоятельство заключено в следующем. Используемая в доказательстве методика основана на предположении, что пары, подлежащие исключению из набора на очередном шаге, распределены примерно равномерно. Однако, это не так. Неравномерность распределения исключаемых пар на каждом шаге обусловлена совместным воздействием процессов исключения на предыдущих шагах. В результате существует вероятность, что на каком-либо из шагов окажется, что в оставшемся наборе имеется больше пар, подлежащих исключению, чем дает оценка для этого шага. И такой эффект действительно, редко, но наблюдается. Так, для четных чисел до 1000 это имеет место примерно в одном случае из ста (388 на шаге 13, 520 на шаге 11 и др.). В этих случаях эффект не влияет на правильность окончательной оценки, однако следует предположить, что на бесконечной числовой оси возможны ситуации, когда пострадает и окончательная оценка. Следует показать, что либо такие ситуации невозможны в принципе, либо внести в выражение, определяющее оценку, коррективы, позволяющие их учесть. Может быть, это просто. А может быть, такие коррективы будут сами по себе являться завуалированной формой Догадки Гольдбаха, или приведут к падению оценки меньше 1, или просто не существуют. Ответ, скорее всего, следует искать на пути анализа взаимодействий большого количества периодических процессов.
