Пролетая над миллионом баксов
Догадка Гольдбаха подтверждается не абсолютно строго, но абсолютно убедительно. Дальше будет приведено полное доказательство, это не шутка. Но сначала предыстория, вдруг кто-нибудь из посетителей перед десертом любит чего-нибудь сладенькое?
Вернее, предысторий две. Первая давняя. Говорят, что ей 258 лет. Так оно и есть.
| Леонард, брателло! В довесок к той цистерне бензина, которую я закинул тебе на прошлой неделе, отгоняю еще вагон селедочных голов, как договаривались. С бабками не тяни, переведи их на тот счет, который я тебе тогда у Муськи дал. Как у тебя дела? Не достает ли Починок? Ну, бывай, на той неделе свидимся. Твой кореш Христиан. 7.06.1742 P.S. Кстати, тут я давеча задумался: а не является ли всякое четное число суммой двух простых чисел? По-моему, так оно и есть. А ты как думаешь? |
Так (или примерно так) писал своему другу великому шведу Леонарду Эйлеру Христиан Гольдбах. Именно постскриптумом он и стал знаменит. Во всяком случае, в Grolier есть статья "Goldbach's Conjecture", а вот статьи "Goldbach" нет.
Загнал ли Эйлер селедочные головы, история умалчивает. А вот на догадку внимание обратил, и с Гольдбахом согласился, но доказательства этому утверждению так и не нашел. Чувствовал, что задачка тривиальная, все думал: как-нибудь; да, видно, некогда было, замотался.
Шли годы. Эйлер закончил свои дела в этом мире, Гольдбах тоже, но люди про догадку не забыли. Уж больно привлекательны такие задачи: на первый взгляд элементарные, а решение в руки не дается. А задумаешься чуть поглубже - и вот уже два мужика в халатах тащут тебя, болезного, по белому коридору на очередной сеанс электрошока.
С годами слово "Догадка" стало писаться с большой буквы, из уважения к труду многих поколений психиатров. Сначала еще теплилась надежда, что кто-нибудь успеет доказать ее раньше лоботомии, но с появлением компьютера угасла: люди стали стремительно разучиваться думать. Зато много народу с большим удовольствием стало гонять процессоры на предмет эмпирических проверок. Дошли до 1014 (вот это тема для диплома! Блеск!).
Некоторое оживление в историю Догадки привнесло появление научной криптографии, поскольку криптографы, будучи людьми ленивыми, очень полюбили простые числа и не захотели возиться со сложными. Но и криптографы, занятые бегом по кругу в поисках ядов и противоядий, приняли Догадку как должное и не стали очень уж надрываться ее подтверждением.
Так и дошло дело до наших дней.
Вторая предыстория - продолжение первой. В 1992 году греческий писатель Апостолос Доксиадис написал роман "Дядя Петрос и Догадка Гольдбаха" (Uncle Petros and Goldbach's Conjecture by Apostolos Doxiadis)
Роман начинается так: "В каждой семье есть своя черная овца - в нашей ею был дядя Петрос". Рассказчик - любимый племянник дяди Петроса. Семейство всегда считало Петроса неудачником. В начале рассказа племянник оглядывается назад, в годы своей учебы в средней школе в Афинах. Тогда его живой детский интерес вызывал эксцентричный дядя, отшельником живший в предместье и интересовавшийся только шахматами и озеленением. Племянник знал, что дядя Петрос когда-то был талантливым математиком, долгие годы учился и преподавал в университете в Германии и немного - в Кембридже. Однажды он приходит к дяде и объявляет, что хотел бы делать карьеру математика. Дядя Петрос предлагает племяннику решить одну математическую задачку. Если решит - то это будет означать, что математика действительно является его призванием. А если не сможет - то должен дать обещание навсегда забыть о математике. Племянник принимает условие, и, так и не найдя решения, по достижении совершеннолетия все-таки отправляется в университет в США в полной неуверенности в своем будущем математика. Его случайный попутчик, оказавшийся математиком, объясняет ему, что задача, заданная ему дядей, была ничем иным, как Догадкой Гольдбаха. Оказалось, что дядя потратил всю свою жизнь в поисках ее доказательства, но так и не нашел его. Во второй части романа читатель видит рассказчика вернувшимся в Грецию и требующим у дяди объяснений: почему тот задал ему неразрешимую задачу. И тогда мы добираемся до "Истории дяди Петроса Папахристоса", которую рассказчик подает нам в третьем лице. Это очаровательная история о математике и гениальности, о гордыне и навязчивой идее, которые все вместе составили жизнь дяди Петроса. Третья часть романа переносит нас в наши дни. Петрос теперь 80-летний старик, и слегка не в себе. Племянник, все-таки начавший свою математическую карьеру, но впоследствии оставивший ее, вновь пытается получить от дяди ответ на вопрос, который не получил когда-то. И далее следует очаровательный конец повествования с великолепной кульминацией. Доксиадис - удивительный рассказчик. Он побуждает вас переворачивать страницы одну за другой, раскрывая вам историю и мир ученого-математика, всю свою жизнь целеустремленно преследовавшего единственную цель: подтверждение Догадки Гольдбаха. А это, между прочим, самая простая и самая трудная из догадок: каждое четное число, большее 2, представляет собой сумму двух простых чисел. Звучит элементарно, неправда ли? (© J.A, перевод assembler.ru)
В этом году роман, по случаю слегка переработанный автором, опубликован на английском языке сразу в США и в Великобритании, двумя издательствами - Faber and Faber Limited (Лондон) и Bloomsbury Publishing (Нью-Йорк). И для того, чтобы сделать потенциальному бестселлеру необходимую рекламу, кто-то из сотрудников того или другого издательства предложил гениальный ход: бросить челлендж ценой в пресловутый миллион баксов. Тогда казалось, что никто особо ничем не рискует (жалко будет, если человека теперь уволят), ведь над подтверждением Догадки Гольдбаха люди бьются сотни лет, и до сих пор даже не уверены, что таковое существует. Насчет увольнения сотрудника - шучу, конечно. Они ведь тоже не лыком шиты. Никто никого не уволит и никакого миллиона никто никому не заплатит, так что ежели кто уже точит фомку, чтобы вскрывать мой пуленепробиваемый сейф, оставьте железо в покое. Правила вызова составлены из того предположения, что потенциальные разгадчики загадки Гольдбаха живут исключительно либо на территории США, либо на территории Великобритании. Как будто если Догадку докажет не-американец или не-англичанин, то это как бы и не будет никаким доказательством. Ну да им виднее.
Так не доставайся ж ты никому! Этой публикацией я нарушаю все правила вызова, установленные издательством, но уж постараюсь сделать так, чтобы мой миллион было бы трудно присвоить кому-нибудь шустрому. Впрочем, все возможно. В правилах же не сказано, что миллион будет вручен автору. Там сказано, что миллион будет вручен выполнившему условия. Эй, резиденты США и Великобритании, для вас еще не все потеряно! В английском языке то, что я сейчас делаю, определяется идиомой "vsju malinu obossal, gad". Впрочем, шутки в сторону. Вот доказательство истинности Догадки Гольдбаха. Примечание от 30.05.00: На самом деле, то что вы можете прочитать далее - это только первый, несовершенный, вариант. Возможно, он будет полезен для понимания основных идей, но его недостатки не позволяют считать его настоящим доказательством. Настоящее сухое математическое доказательство здесь. Примечание от 27.07.00: Еще более сухое и, возможно, более корректное (или истинное, чем черт не шутит?) доказательство Догадки прислал Тим Туманный. Читайте!.
Еще раз повторю формулировку Догадки:
"Каждое четное число, большее двух,
может быть представлено
в виде суммы двух простых чисел."
Для начала поговорим о природе простых чисел. Всякому, кто когда-нибудь интересовался простыми числами, знакомо чувство удивления, которое вызывает видимая бессистемность их расположения в числовом ряду. Казалось бы, про ряд натуральных чисел люди должны знать все, ведь это самые первые числа, с которыми познакомились наши пращуры сразу после того, как однажды на охоте завалили не одного мамонта, а двух. И вот в этом незыблемом от Начала Времен монолитном строю, оказывается, полным-полно бойцов, которые стоят где хотят, и совершенно непонятно, как они там оказались.
Причем любой здравомыслящий человек, конечно же, понимает, что никакого хаоса нет, и вот это-то и раздражает больше всего. Если нет хаоса - значит, есть система. Видимо, сложная, но все-таки система. Так в чем же она?
Для ответа на этот вопрос, и раз уж мы обсуждаем натуральные числа, самое время вспомнить о кирпичах.
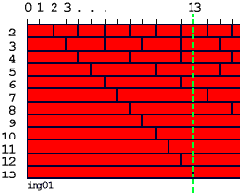
Нарисуем все потенциальные делители так, как показано, в виде кирпичной кладки.
Идея, по-моему, достаточно очевидна. Например, делитель "2" укладывается в кладке до отметки "13" шесть раз целиком, и еще пол-кирпича торчат наружу. А вот делитель "3" - четыре раза целиком и еще кусочек. И так далее.
Мы видим, что на отметку "13" попадает стык кирпичей в одном-единственном ряду - в ряду "13". Не нужно быть бакалавром математики, чтобы сообразить, что смысл этого рисунка, если исключить из рассмотрения избыточный нижний ряд, можно сформулировать следующим образом: "Если на отметку числа не попадает ни один стык кирпичей, то оно простое".
Теперь приглядимся к кладке повнимательнее. Посмотрите: все стыки в ряду "4" попадают на стыки в ряду "2"! Это значит, что если тестируемое число не попадает на стык в ряду "2", то уж на стык в ряду "4" оно точно не попадет! А мы, дураки, мучились, раствор мешали, на прораба матерились... Оказывается, ряд "4" совершенно неинтересен в смысле тестирования чисел на предмет их простоты. Убираем его нафиг. А вместе с ним и ряды "6", "8", "9", "10" и "12", так как все их стыки тоже надежно совпадают со стыками вышележащих рядов. Смотрим, что получилось.
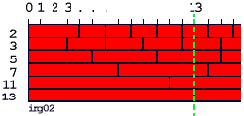
Мама дорогая! Так это ж все сплошь простые числа! Вот оно, первое гениальное прозрение вольного каменщика: "Чтобы выяснить, является ли число простым, достаточно установить отсутствие его делимости нацело на все простые числа, меньшие его."
Уважаемые товарищи программисты! Не загружайте процессоры бесполезной работой! При определении простоты чисел используйте в качестве делителей только простые числа! (За исключением случаев, когда вы пишете на JavaScript. Тогда вы можете на этот призыв наплевать - все равно скрипт работает на чужом компьютере. Именно так я и сделал в этом примере.)
Впрочем, все вышесказанное никаких откровений в себе не содержит и давно всем очевидно. Не волнуйтесь: это всего лишь подготовка строительной площадки. А вот теперь, еще раз хорошенько всмотревшись в кирпичи, мы готовы сделать действительно принципиально важное для доказательства Догадки Гольдбаха умозаключение. Вот оно:
Простое число есть совокупный продукт
от всех простых чисел, меньших его.
Каждый ряд в кирпичной кладке - это периодический процесс с длиной периода, равной соответствующему ему простому числу. В точке 0 числовой шкалы узлы всех периодов совпадают. Очередное простое число образуется в точке, в которой периоды всех предыдущих простых чисел не имеют узлов. Следующее простое число образуется в новой точке, зависящей не только от всех предыдущих простых чисел, но и от вновь найденного.
Не удивительно, что ни на первый, ни на второй взгляд невозможно обнаружить системы в расположении простых чисел в числовом ряду! Ведь каждое простое число - это каша из всех предыдущих, тем более перемешанная и многокомпонентная, чем дальше от начала координат мы находимся.
Из этого тезиса можно делать разные полезные выводы, впрочем, имеющие отдаленное отношение к теме. Например, можно смело утверждать, что не может существовать никаких других строгих правил определения произвольного простого числа, кроме полного перебора всех простых чисел, меньших его.
И вот теперь, разобравшись с природой простых чисел, вернемся собственно к Догадке, и, конечно же, к кирпичам. Разве что раскрасим их теперь в какие-нибудь веселенькие цвета.
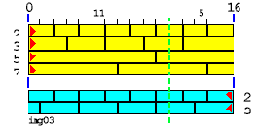
На этом рисунке слагаемое 11 покрашено в желтый цвет и представлено не само собой, а совокупностью формирующих его рядов кирпичей, соответствующих меньшим простым числам. Кирпичи, составляющие же слагаемое 5, покрашены в голубой цвет. Кроме того, начало кладки голубых кирпичей мы перенесли в точку "16", и направили кладку навстречу желтой. Видим, что имеет место точка рандеву, в которой встречаются отложенное слева число 11 и отложенное справа число 5. В этой точке, в соответствии с изложенным выше кирпичным взглядом на природу простых чисел, ни в одном ряду нет стыка кирпичей.
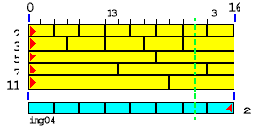
Почему сказано "вариант кладки" - потому что возможны и другие варианты, как показано на рисунке справа.
Давайте еще раз рассмотрим рисунок img03, ибо он позволяет сформулировать условие существования точки рандеву. Видно, что существует 15 точек, каждая из которых потенциально может стать точкой рандеву. Но всем, кроме одной, мешают стыки рядов кирпичей, иногда одного, а иногда и сразу нескольких. Разберемся с каждым из рядов по отдельности.
Правда, на рисунке img04 есть еще точка, отстоящая слева на 1, а справа - на 15, которой не мешает ни один стык кирпичей. Такая точка имеется у всех пар простых слагаемых, одно из которых - 3. Существование этой точки еще ждет своего объяснения, и, я думаю, кирпичная теория простых чисел способна дать его.
Видно, что желтый и голубой ряды кирпичей "2" синфазны. Их стыки совпадают. Это не удивительно, ведь число 16 кратно 2. Эти ряды будут совпадать и для любых других четных чисел. И они отсеивают половину всех потенциальных точек рандеву. Если бы фазы голубого и желтого рядов "2" не совпадали, тогда совместными усилиями они бы отсеяли все точки. Однако фазы рядов "2" не совпадают только у нечетных чисел.
А вы-то, небось, думали, что нечетное число не может быть суммой двух простых чисел, потому что сумма двух нечетных всегда четна? На самом-то деле причина в кирпичах!
А вот ситуация с желтым и голубым рядами "3" гораздо интересней. Поскольку число 16 не кратно 3, то фазы этих рядов не совпадают. В результате ряды "3" еще отнимают каждые две из трех потенциальных точек рандеву, оставшихся после разгрома, учиненного рядами "2". Очевидно, что после их совместных усилий остается вот какая доля потенциальных точек рандеву:
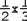
Следующий ряд - "5". К сожалению, на рисунке img03 ситуация не очень удачная - нет голубого ряда "5", потому что число 16 слишком маленькое. То же касается и ряда "7". Впрочем, мы уже достаточно подготовлены, чтобы забросить возню с кирпичами и обратиться-таки к абстрактным рассуждениям.
Если бы исследуемое четное число было побольше, и у второго слагаемого был бы голубой ряд "5", то он бы мог быть синфазен желтому (например, для числа 20), или несинфазен (например, для числа 22). Будем ориентироваться на худший для нас второй случай. Рассуждая аналогично рядам "3", можно считать, что несинфазные ряды "5" оставят только 3 из 5 точек, оставшихся после совместного воздействия рядов "2" и "3". То есть доля оставшихся потенциальных точек рандеву будет:
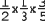
Аналогично для рядов "7":
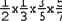
Очевидно, зависимость доли остающихся потенциальных точек рандеву от числа рядов образует прогрессию. Каждый очередной ее член формируется путем умножения предыдущего на величину, определяемую очередным простым числом, то есть зависит сразу от всех предыдущих простых чисел и от текущего. (Обратите внимание, насколько это согласуется с природой простых чисел, которую мы обсуждали выше!) Первый член этой прогрессии - 1/2. Остальные в общем виде можно записать так:
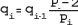
Здесь:
- qi - очередной (i-й) член прогрессии
- Pi - соответствующее этому члену простое число из ряда простых чисел, начиная с 2
Также очевидно, что прогрессия (4) бесконечно стремится к 0.
Сформулируем достаточное условие существования точки рандеву: "Для того, чтобы для некоторого четного числа Ej существовала хотя бы одна точка рандеву, достаточно, чтобы интерполированное значение прогрессии qi при Pi близком к половине Ej было не меньше, чем значение прогрессии:
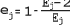
Поясним, откуда здесь что.
(Ej-2)/Ej - это максимальная доля точек, которые не должны являться точкой рандеву для того, чтобы существование точки рандеву стало возможным. Наверное, проще пояснить на примере. Смотрим рисунок img03. Здесь Ej=16. Число потенциальных точек рандеву - 16-1=15. Но существование хотя бы одной точки рандеву возможно лишь в том случае, если не-"точками рандеву" будут не более 16-2=14 из них. То есть их максимальная доля составляет 14/16.
1-(Ej-2)/Ej - это, следовательно, минимально необходимая доля действительных точек рандеву (то есть доля одной-единственной точки).
Наконец, почему Pi должно быть близко к половине Ej? Да потому, что Догадка как раз про это: про четное как сумму двух простых. И еще вот почему.
Как уже было сказано, нас интересуют наихудшие для существования точек рандеву случаи. Если в этих случаях условие существования выполняется - то уж во всех других оно будет выполняться точно. Случай, когда простые слагаемые близки к половине составляемого ими четного числа, как раз из таких. Количество желтых и голубых рядов кирпичей в этих случаях примерно равно, в результате чего складываются наиболее благоприятные возможности для появления их несинфазности. Кстати, именно для таких, а вернее, для предельно худших случаев составлена прогрессия (4), потому что она вообще не предполагает наличия синфазных рядов (кроме, естественно, ряда "2").
Ну что ж, осталось совсем немного: убедиться, что достаточное условие существования точки рандеву действительно выполняется. Щелкайте - и убеждайтесь.
Убедились? Есть вопросы, да? Первый бросается в глаза сразу: почему в начальной части qi < ej? Ну что ж, если вы хотите проверить, что в этой части каждое четное число имеет пару простых слагаемых, просто посчитайте, это нетрудно (или поверьте предыдущим поколениям математиков). А насчет правоты достаточного условия - так оно ведь достаточное, а не необходимое. Здесь оно не работает по двум причинам. Во-первых, помните, что прогрессия (4) составлена в расчете на худший из худших случаев, когда голубых и желтых рядов - примерно поровну. Если вы учтете для первых нескольких чисел конкретные более благоприятные расклады (это выразится в замене в выражении (4) двойки на единицу в случае синфазности соответствующих рядов), весьма вероятно, все встанет на свои места. И во-вторых, на начальном участке велико влияние краевого эффекта, ведь наше достаточное условие в некотором роде - статистическое, и плохо работает на небольших выборках. Последнее утверждение, конечно же, образное. На самом же деле краевой эффект проявляется в том, что при небольшом числе младших простых чисел, определяющих слагаемые, на значение прогрессии (4) большое влияние оказывают дробные части от деления Ej на младшие простые числа (грубо говоря, части кирпичей, выступающих наружу).
Правда, насчет краевого эффекта - это просто догадка. Есть ли он на самом деле, и в какую сторону он влияет, я не анализировал, потому что задача эта громоздкая и в нашем контексте бессмысленная.
Второй вопрос возникнет у тех, кто разберется в программе. Она составлена "наоборот": мы не задаемся четными Ej, подбирая потом подходящие Pi, а последовательно перебираем Pi и получаем из него Ej простым умножением на 2. На самом деле, никакого вопроса здесь нет: нам достаточно построить кривые, а как - это безразлично. Нам даже все равно, четные ли числа Ej.
Если быть до конца честным, то получаемые с помощью выражения (4) значения прогрессии qi - это не самые минимальные из возможных значений минимальной доли точек рандеву, но они очень близки к минимальным, и ими вполне можно пользоваться для проверки достаточного условия существования точки рандеву. Причем, чем дальше по числовой оси, тем с большей надежностью. Убедиться в этом можно с помощью примера, который вычисляет реальные доли потенциальных точек рандеву для пар простых чисел, подозрительных на то, что они дают в сумме заданное четное число. Сохраните пример на диск и попробуйте поиграть с переменной ej, давая ей разные четные значения. Видно, что значения долей для этих пар образуют седло, и результат вычисления выражения (4) всегда находится в его нижней части. Извините за невнятность примера, но это - факультативная информация.
Кстати, вот еще один пример, позволяющий убедиться в справедливости нашего метода. Здесь сравнивается реальное количество пар простых слагаемых для каждого четного числа (Npairs) и прогнозируемое с помощью прогрессии (4) минимальное количество точек рандеву (qi*Ej). Совершенно однозначно видно, что после преодоления краевого эффекта ожидаемое минимальное количество точек рандеву надежно меньше, чем реальное число пар, но, конечно же, больше 1. То есть наша оценка действительно учитывает вариант "хуже худшего", но показывает, что всегда имеется не менее одной пары простых слагаемых.
Итак, мы убедились, что ej стремится к 0 гораздо быстрее, чем qi. Догадка Гольдбаха верна и подтверждена.
В заключение несколько замечаний.
Первое - философское. Обратите внимание НАСКОЛЬКО ej быстрее стремится к 0. И это, учтите, при наихудших условиях! Поэтому Догадка - это ОЧЕНЬ сильный закон. И, наверное, в этой силе - пролог ее мистической истории. Вот почему она буквально бросилась в глаза Гольдбаху (а если быть точным - то еще Декарту) во времена, когда простые числа не могли иметь никакого практического приложения и интересовали разве что чудаков. Вот почему люди искали, ищут и будут искать ясное и строгое ее доказательство: им просто не верится, что у такого сильного закона может его не оказаться. А с практической точки зрения эта сила проявляется в том, что пары простых слагаемых в подавляющем большинстве случаев обнаруживаются уже в непосредственной близости от половины четного числа. Убедитесь!
Второе - конкретное. Как видим, приведенное доказательство истинности Догадки нельзя считать абсолютно строгим. А возможно ли действительно строгое доказательство? Ответ: нет! Все те люди, включая дядю Петроса, кто потратил свои жизни на поиск доказательства, на самом деле строили вечный двигатель. Дело в природе простых чисел. Каждое очередное простое число ортогонально всем предыдущим и как бы создает новый мир, в котором не действуют законы предыдущих миров. И уж тем более для всех этих миров нет единого закона. Как невозможно точно выяснить, является ли взятое наугад нечетное число простым, не перебрав все предыдущие простые числа, так невозможно строго подтвердить Догадку.
Третье - эмоциональное. Печальное завершение романтической истории, правда? Так хотелось, чтобы у Догадки было такое же простое и красивое доказательство, как она сама: полтора десятка слов, и ничего не добавишь и не выкинешь... Вместо этого - кирпичи и приблизительные оценки. Жаль...
